堆排序

堆排序

堆

完全二叉树

每个节点大于或者等于左右孩子 - 大顶堆

每个节点小于或者等于左右孩子 - 小顶堆

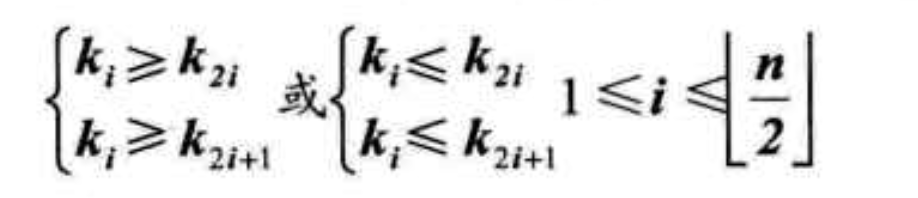
以数组存储为例：

1. 如果i=1,节点i为二叉树的根；如果i>1, 则双亲节点
2. 如果i.1, 则\(\lfloor n/2 \rfloor\)为双亲节点
3. 下标i，孩子节点为 2i 和 2i+1

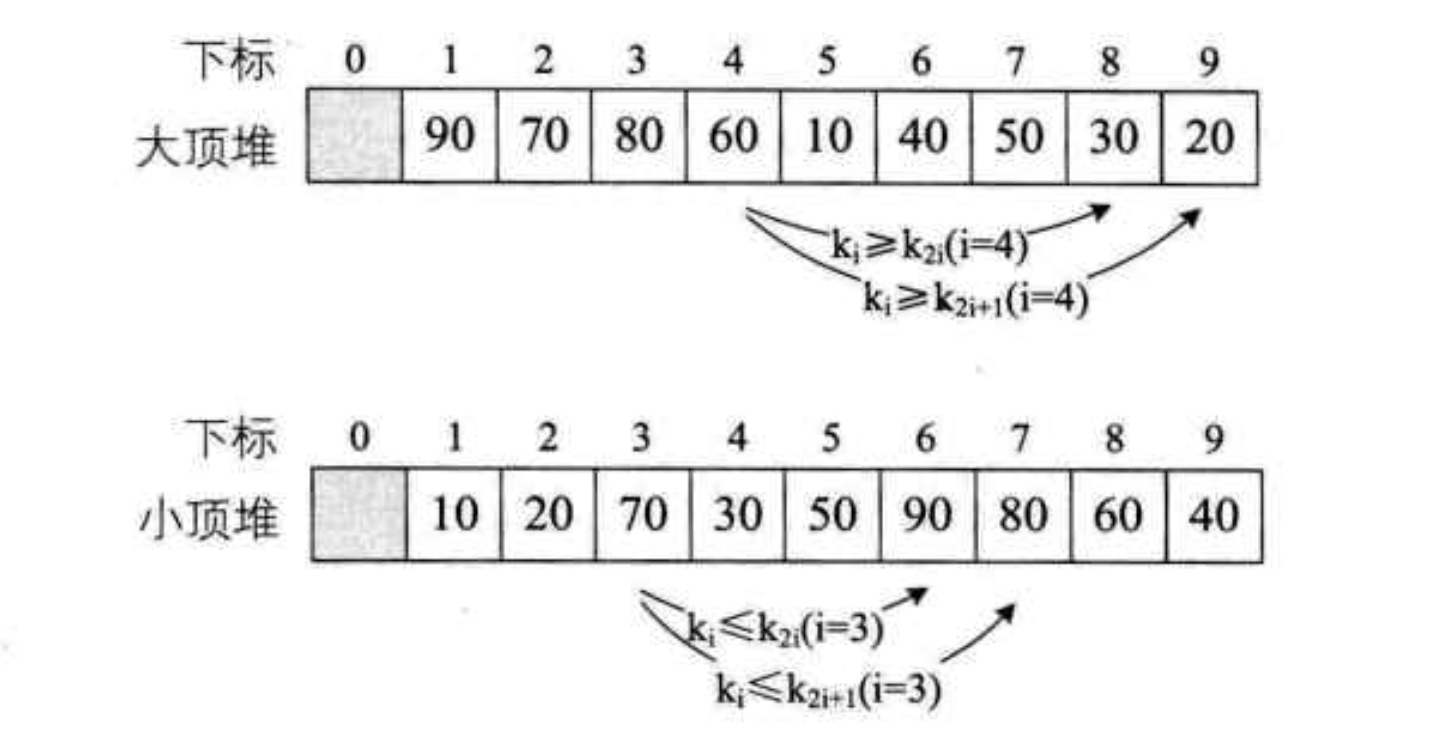
堆排序

• 先构造成大顶堆
• 将堆顶移走（和堆数组末位元素交换），然后将剩余的n-1个序列重新构造成堆。

关键：如何将无序序列构造成堆？堆顶输出后如何调整剩余元素为一个新的堆？

---

代码

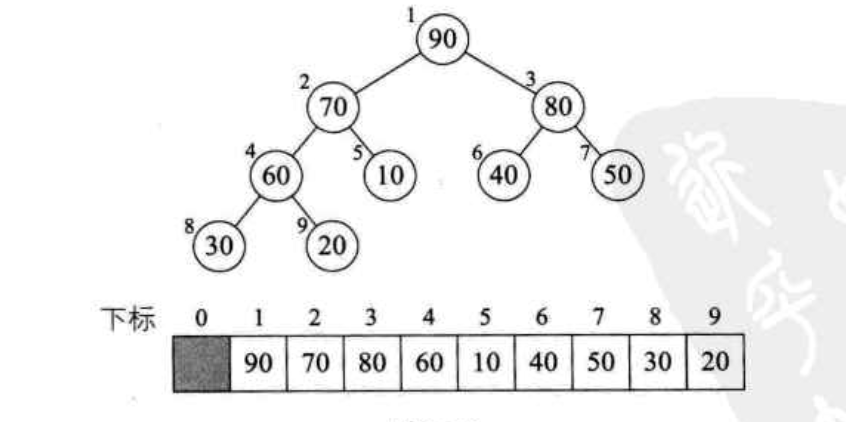
public class HeapSort {

    public static void heapSort(int[] input) {
        int length = input.length;
        int i;
        for (i = length / 2; i > 0; i--) {
            /**
             * 构建大顶堆，从下往上将每个非叶子节点当做根节点，将其和其子树调整成大顶堆
             *
             */
            heapAdjust(input, i - 1, length - 1);
        }

        // 堆排序，依次将堆顶元素调整至数组尾部，剩余元素重新调整为大顶堆
        for (i = length - 1; i >= 0; i--) {
            swap(input, 0, i);
            heapAdjust(input, 0, i - 1);
        }

    }

    private static void heapAdjust(int[] input, int start, int end) {

        int tmp = input[start];
        for (int j = start * 2 + 1; j <= end; j = j * 2 + 1) {
            if (j < end && input[j] < input[j + 1]) {
                j++;
            }
            if (tmp >= input[j]) {
                break;
            }
            input[start] = input[j];
            start = j;
        }
        input[start] = tmp;

    }

    private static void swap(int[] input, int i, int j) {
        int tmp = input[i];
        input[i] = input[j];
        input[j] = tmp;
    }
}

总结

时间复杂度\(O(nlg_n)\) ¹

空间复杂度，只需要一个用来做为交换单元

由于构建堆需要较多比较次数，不适合待排序序列个数较少的情况

---

1. 利用了二叉树树的深度： \(\lfloor log_2n \rfloor\)↩︎