快速排序

快速排序

快速排序的核心思想也是分治法， 20世纪十大算法之一。

交换类排序改进算法（冒泡算法）

基本思想

quicksort

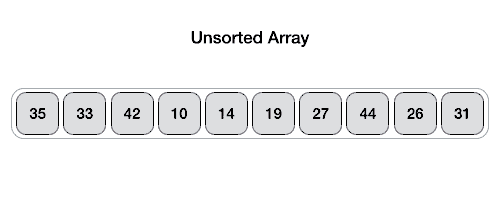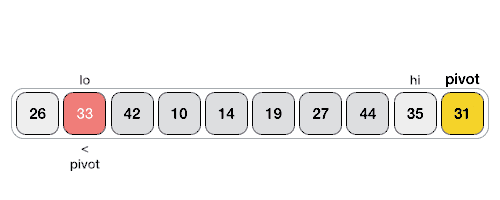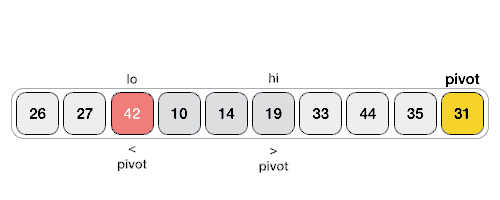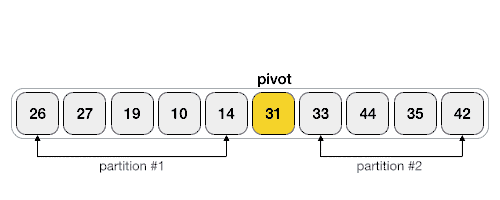
通过一趟排序将待排记录分割为独立的两部分，其中一部分 关键字均比另一部分关键字小，分别对两部分继续排序，最终达到整体有序。

• 从数列中挑出一个元素，称为 “基准”（pivot）；
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

核心： partition

partition，选取一个关键字（pivot），左边值都比pivot小，右边值都比pivot大。

代码

public class QuickSort {

    public static void quickSort(int[] array) {
        doSort(array, 0, array.length -1);
    }


    private static void doSort(int[] array, int startIndex, int endIndex) {

        if (startIndex >= endIndex) {
            return;
        }

        int pivotIndex = partition(array, startIndex, endIndex);
        doSort(array, startIndex, pivotIndex -1);
        doSort(array, pivotIndex +1, endIndex);

    }

    private static int partition(int[] arr, int startIndex, int endIndex) {

        int left = startIndex;
        int right = endIndex;
        int pivot = arr[startIndex];

        while(left < right) {

            while (left < right && pivot <= arr[right]) {
                right --;
            }
            swap(arr, left, right);

            while(left < right && pivot >= arr[left]) {
                left ++;
            }
            swap(arr, left, right);
        }

        return left;
    }

    private static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

}

快速排序的优化

1. 选取pivot

目前是选取第一个元素作为pivot，第一个元素太小或太大都会影响partition，因此固定选取第一个位置的值作为pivot有待改进。

• random
• 三数取中： 去左中右三个数，将中间数作为pivot
• 对于非常大的待排序列，可以选取更多数据取中(eg: 九数取中)

2. 减少交换

提前记录pivot（类似哨兵），需要左右互换是适用替换操作，执行结束，也就是low和high回合时将pivot放置到low的位置

3. 优化小数组

由于快速排序试用递归，数据量大时有优势（递归可忽略不计），但对于几个数据进行排序优势不明显。

判断待排数据数量，如果大于一定阈值，适用快速排序，否则可选择诸如插入排序。

总结

快速排序的时间复杂度取决于递归深度(递归树的深度)。

• 最优情况： 如果partition划分很均匀，递归树深度为\(\lfloor log_2n \rfloor\) + 1, 递归树是平衡的， 总时间复杂度为\(O(nlgn)\)
• 最差情况： 序列已经排好序（无论正序或逆序），每次划分只能得到比上一次少一条记录的子序列，递归树为斜树。时间复杂度为\(O(n^2)\)