学习笔记之回溯

[学习笔记] 回溯 （backtracking）

回溯问题，实际上就是一个决策树的遍历过程

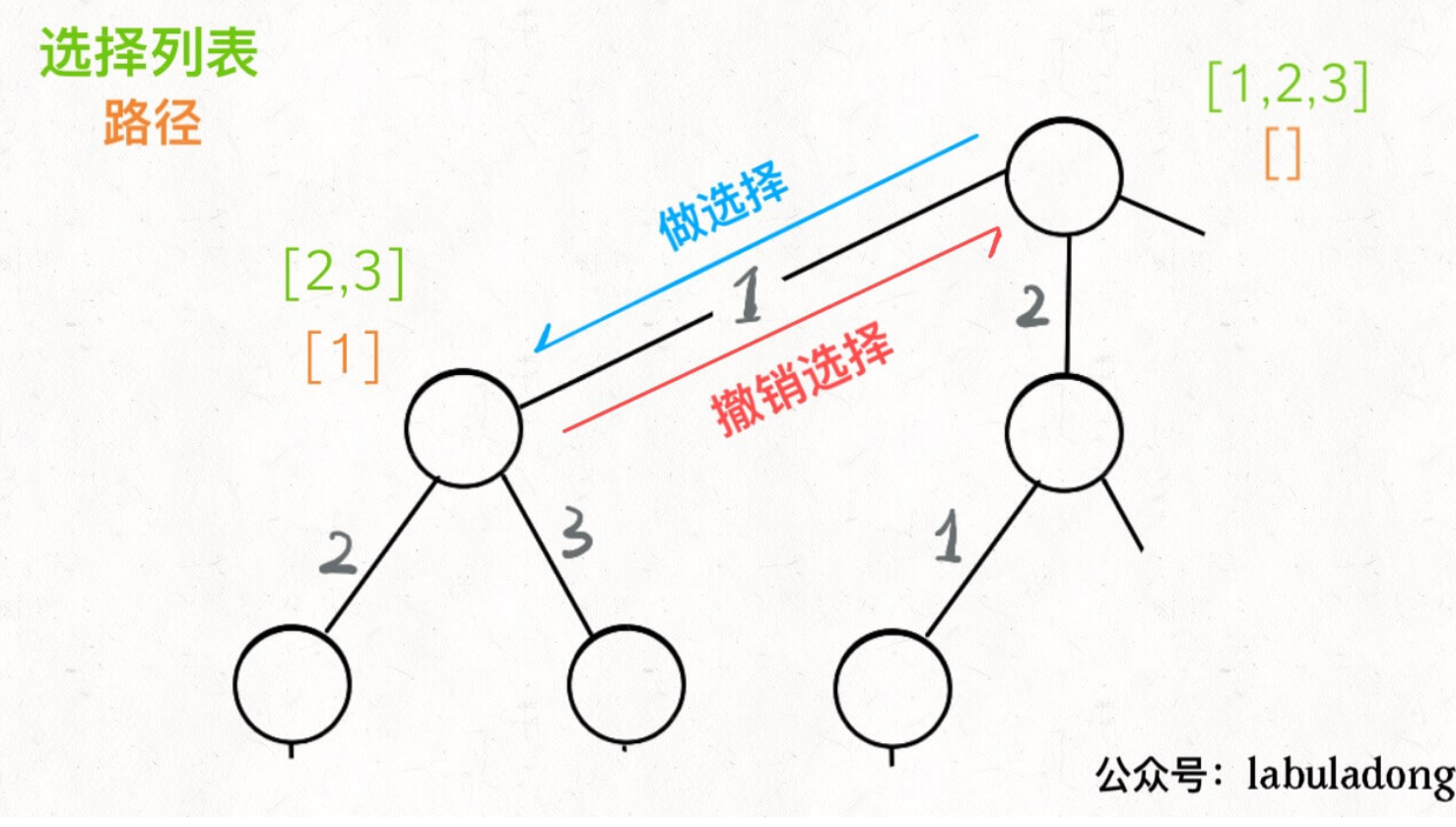
• 路径： 已经做出的选择
• 选择列表： 当前可以做的选择
• 结束条件：到达决策树底部，无法再做选择

代码框架

result = []
def backtrack(路径, 选择列表):
  if 满足结束条件：
    result.add(路径)
    return
  
  for 选择 in 选择列表：
    做选择
    backtrack（路径，选择列表）
    撤销选择
    
    

核心是for 循环中的递归，递归之前做选择，递归之后撤销选择。

全排列问题

穷举全排列。

解题过程：

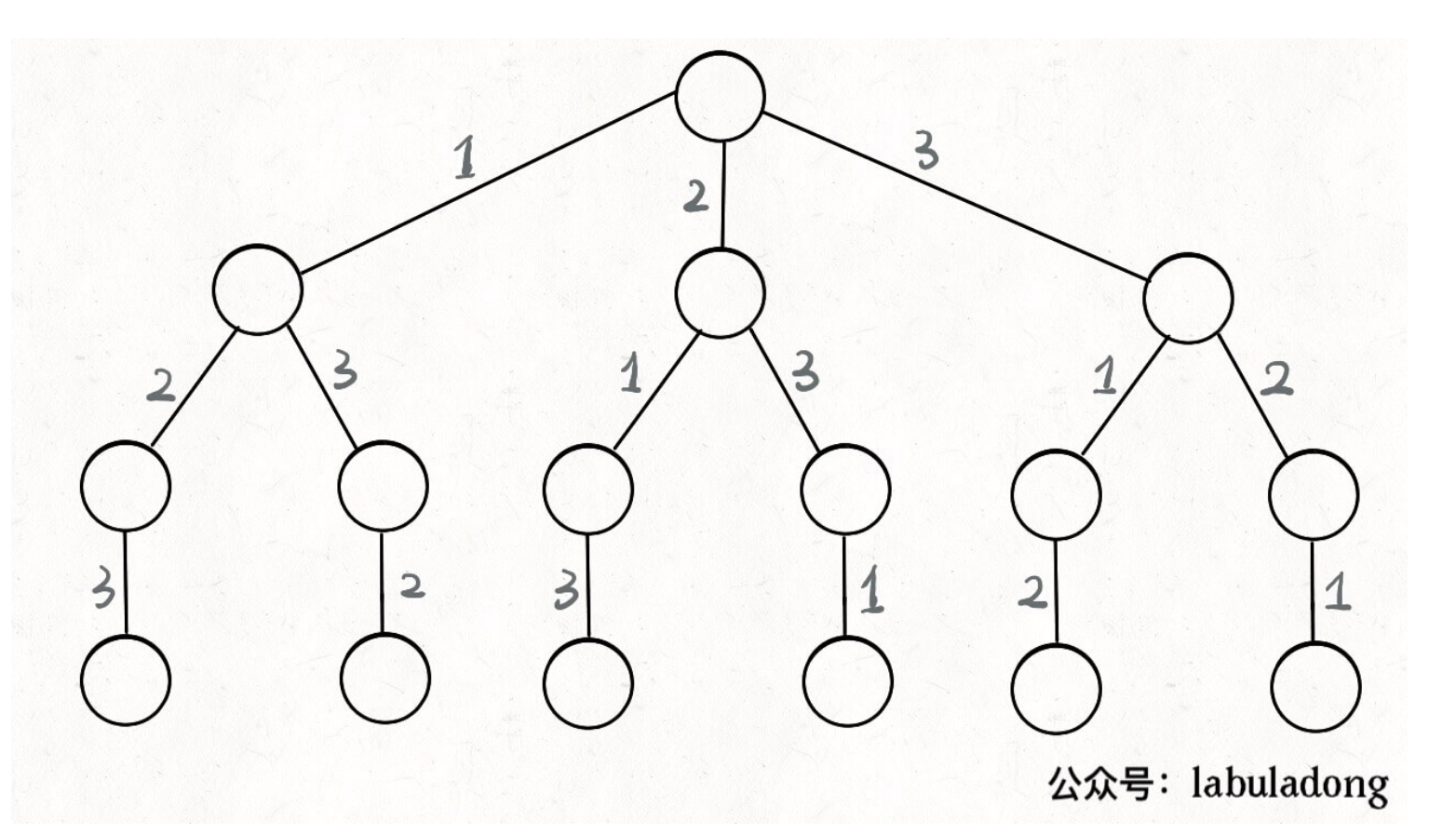
先固定第一位是1，然后第二位可以是2或3， 第二位是2 则第三位只能选3，如果第二位选3那么第三位只能是2；

退回去变化第一位。。。

以上为回溯算法的决策树

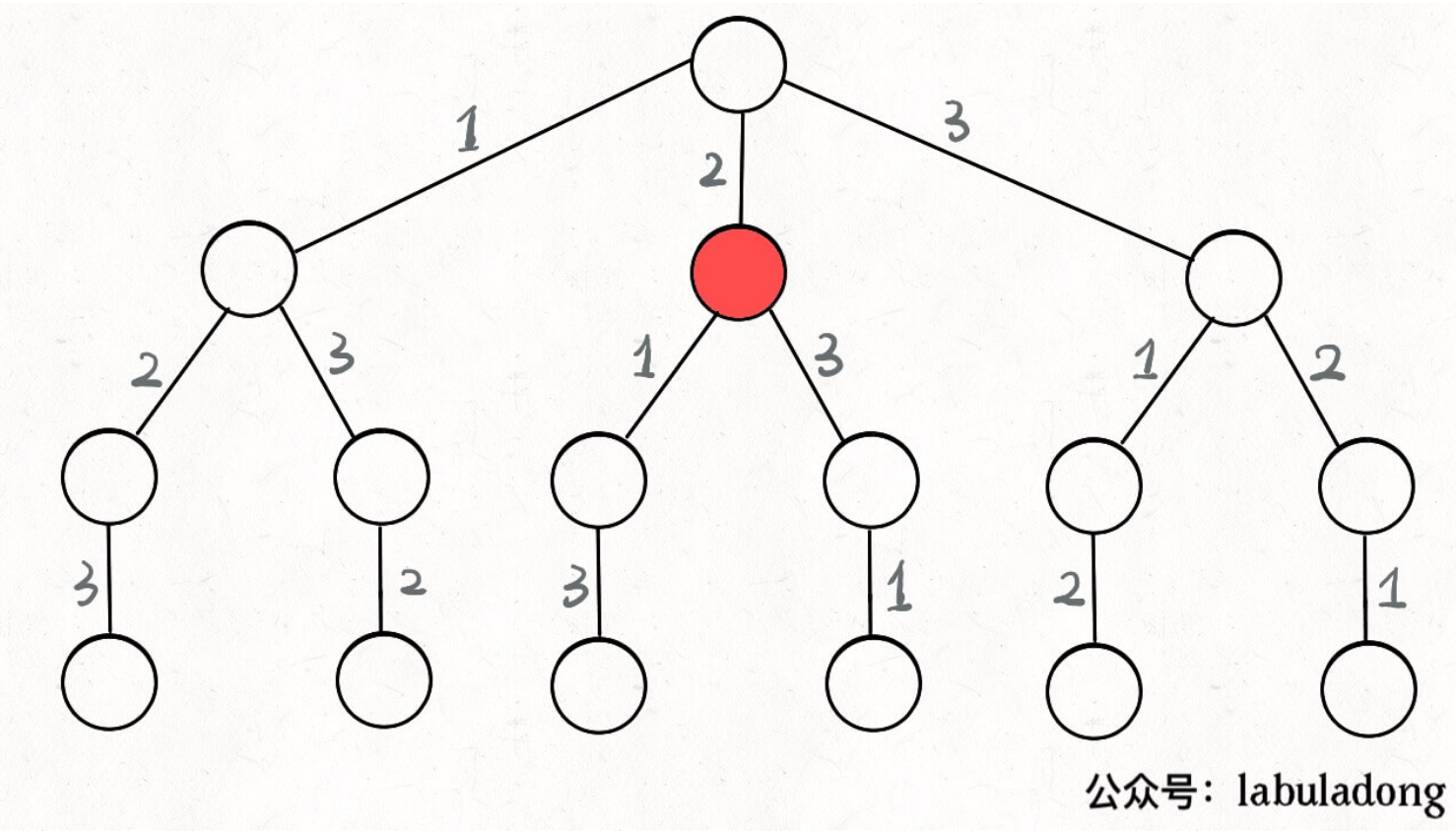
假定在红色节点，可选择1或3（选择列表），2为已经选择过的路径。

结束条件为到达树底部，也就是选择列表为空。

import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;

public class Permutation {

  private static List<List<Integer>> res = new LinkedList<>();

  public static List<List<Integer>>  permute(int[] nums) {
    LinkedList<Integer> track = new LinkedList<>();
    backtrack(nums, track);
    return res;
  }

  private static void backtrack(int[] nums, LinkedList<Integer> track) {
    //  结束条件
    if(track.size() == nums.length){
      res.add(new LinkedList<>(track));

      return;
    }

    for (int i = 0; i < nums.length; i++) {
      // 排除不合法的路径
      if(track.contains(nums[i])) {
        continue;
      }

      // 做选择
      track.add(nums[i]);
      //下一层决策树
      backtrack(nums,track);
      // 取消选择
      track.removeLast();
    }
  }

  public static void main(String[] args) {
    int[] input = {1, 2, 3};
    List<List<Integer>> lists = permute(input);

    for (int i = 0 ; i < lists.size(); i ++) {
      System.out.println("permutation " + i + " : ");
      System.out.println(Arrays.toString(lists.get(i).toArray()));
    }
  }
}

总结

回溯算法

def backtrack(...):
    for 选择 in 选择列表:
        做选择
        backtrack(...)
        撤销选择

backtrack函数，需要维护走过的路径和当前可做的选择列表，当触发结束条件时，将路径计入结果集。

回溯算法时间复杂度都不会低于O(n!), 穷举整颗决策树。而动态规划存在重叠子问题可以优化。

---

参考

https://labuladong.gitbook.io/algo/suan-fa-si-wei-xi-lie/hui-su-suan-fa-xiang-jie-xiu-ding-ban