学习笔记之递归

[学习笔记] 递归

什么是递归

以阶乘为例

public int factorial(int n) {
    if (n < =1) {
        return 1;
    }
    return n * factorial(n - 1)
}

所以递归的本质是能把问题拆分成具有相同解决思路的子问题，。。。直到最后被拆解的子问题再也不能拆分，解决了最小粒度可求解的子问题后，在「归」的过程中自然顺其自然地解决了最开始的问题。

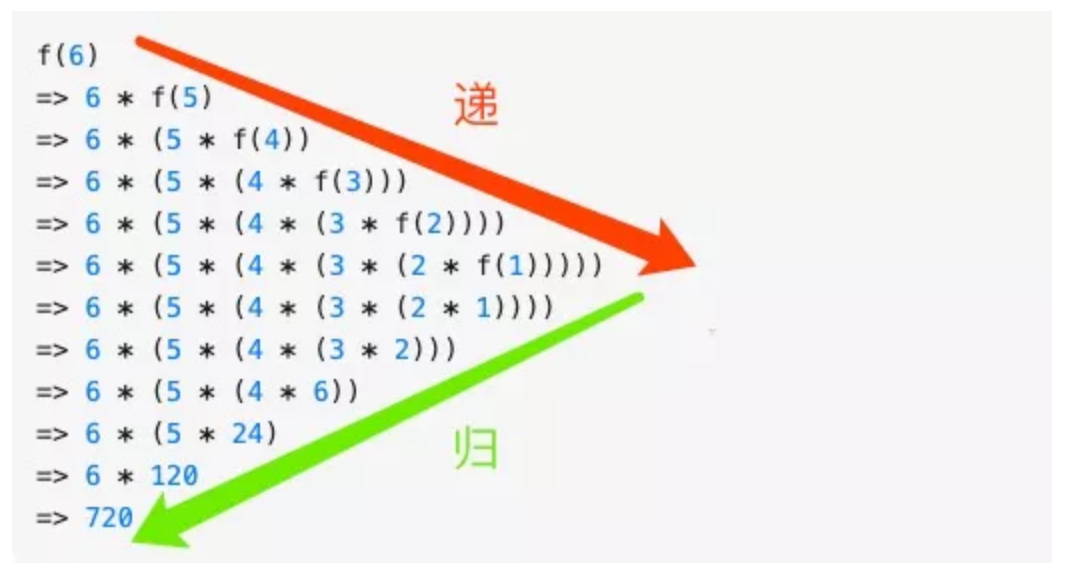
通用解决思路

递归问题的特点：

1. 一个问题可以分解成具有相同解决思路的子问题，子子问题，换句话说这些问题都能调用同一个函数
2. 经过层层分解的子问题最后一定是有一个不能再分解的固定值的（即终止条件）,如果没有的话,就无穷无尽地分解子问题了，问题显然是无解的。

关键点

寻找问题与子问题的关系 - 递推公式 ， 例如f(n) = n * f(n-1) 这个便是阶乘函数的递推公式。

寻找最终不可在分解的子问题 - 终止条件

例题

一只青蛙可以一次跳 1 级台阶或者一次跳 2 级台阶，例如： 跳上第 1 级台阶只有一种跳法：直接跳 1 级即可。 跳上第 2 级台阶有两种跳法：每次跳 1 级，跳两次；或者一次跳 2 级。 问要跳上第 n 级台阶有多少种跳法？

Step1

定义函数

/**
 * 跳 n 极台阶的跳法
 */
public int f(int n) {
}

Step2

递归公式和终止条件

跳到n级台阶只能从n-1 或者n-2 跳，因此问题分解为f(n) = f(n-1) + f(n-2)，当n=1和n=2时，也就是跳第一级台阶和第二级台阶的跳法为1 和2.

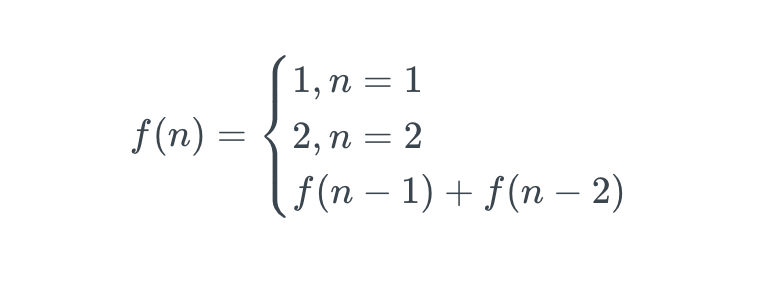
Step3

将递推公式补充到step1中的函数

/**
 * 跳 n 极台阶的跳法
 */
public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    return f(n-1) + f(n-2)
}

优化

递归树

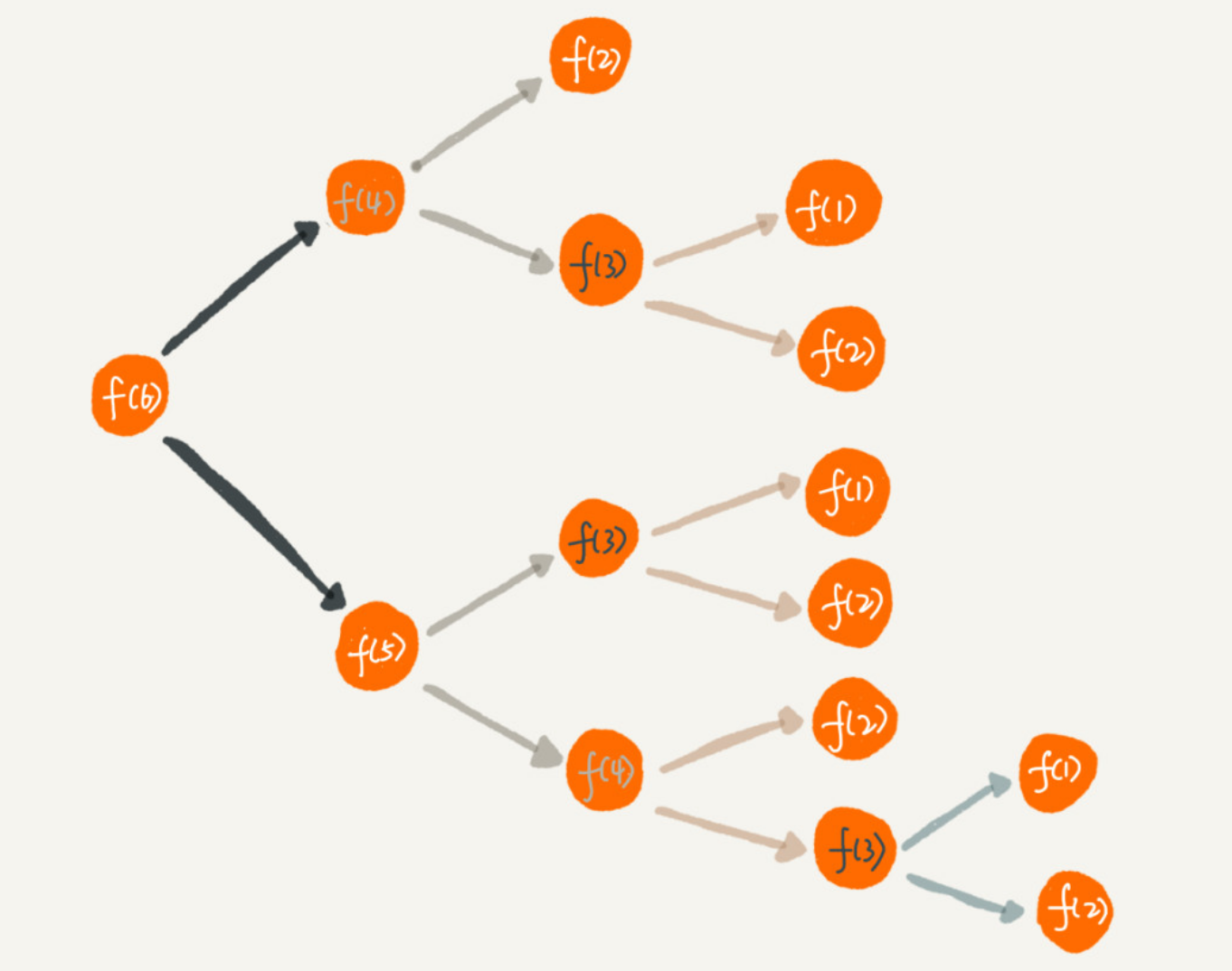
可以看到有大量的重复计算, f(3) 计算了 3 次， 随着 n 的增大，f(n) 的时间度自然呈指数上升了

空间换时间-保存中间计算结果

public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    // map 即保存中间态的键值对， key 为 n，value 即 f(n)
    if (map.get(n)) {
        return map.get(n)
    }
    int result = f(n-1) + f(n-2);
     map.put(n, result);
    return result
}

---

参考

https://mp.weixin.qq.com/s?__biz=MzI5MTU1MzM3MQ==&mid=2247483813&idx=1&sn=423c8804cd708b8892763a41cfcc8886&scene=21#wechat_redirect

https://labuladong.gitbook.io/algo/suan-fa-si-wei-xi-lie/di-gui-xiang-jie