学习笔记之图
[学习笔记] 图
图的定义
概念
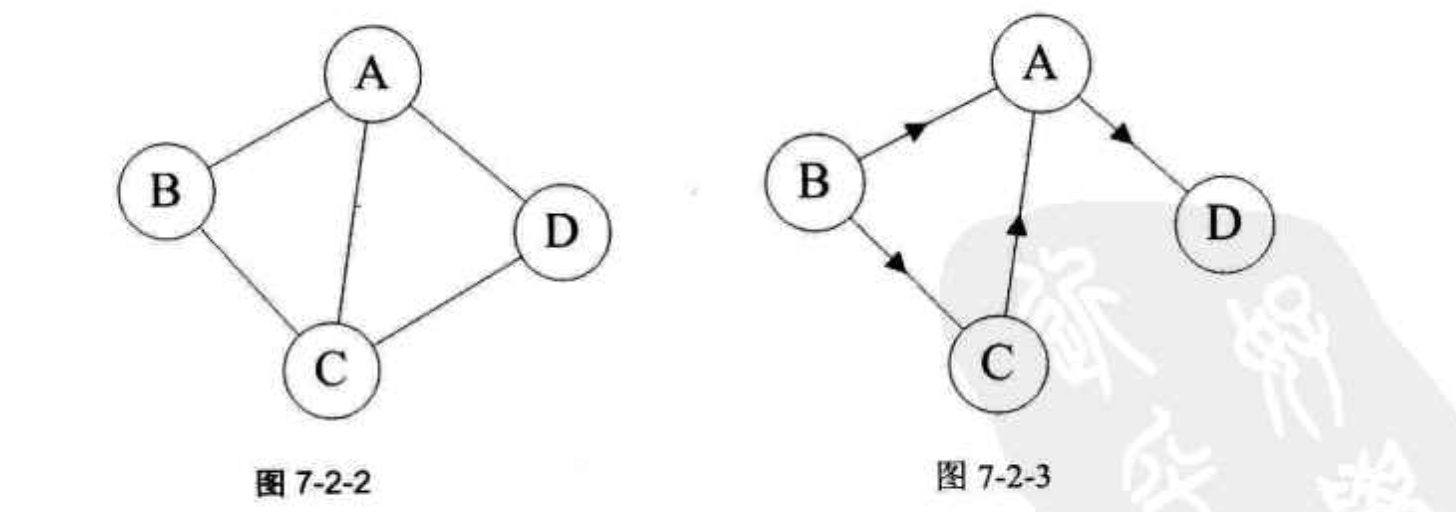
图(graph)是由顶点的有穷非空结合和顶点之间的边的集合组成,表示为: G(V, E), 其中G表示一个图,V(vertex)是图G中顶点的集合,E(edge)是图G中边的集合。
无向边: 若顶点\(v_i\) 到\(v_j\) 之间的边没有方向, 则称之为无向边。使用圆括号表示 无向图: 如果图中任意两个顶点之间都是无向边,那么图称为无向图。
有向边: 若从顶点\(v_i\) 到\(v_j\) 之间的边有方向,称之为有向边,也称为弧(arc)。使用尖括号表示, <A,D>, A是弧尾,D是弧头。 有向图:如果图中任意两个顶点的边都是有向边,该图称之为有向图。
在无向图中,如果任意两个顶点间都存在边,则改图为无向完全图。n个顶点的无向完全图的边数: n*(n-1) /2。
在有向图中,如果任意两个顶点间都存在方向互为相反的两条弧,则该图称为有向完全图。n个顶点的有向完全图的边。数: n*(n-1)
有很少条边或弧的图称为稀疏图,反之称为稠密图(稀疏和稠密是相对的概念)。
图的边或者弧上有关的数 叫 权(weight),带权的图称为网(network)。
图的表示方法
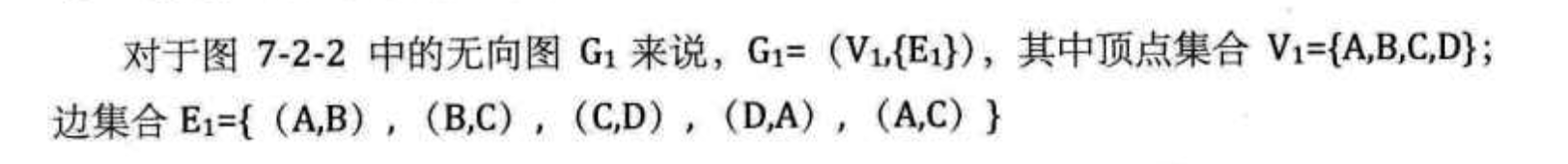
图的顶点与边的关系
无向图G=(V, {E}), 对于边(v,v') ,顶点v和v'互为邻接点,即v和v' 相邻接。边(v,v')依附于顶点v和v', 或者说(v,v')于顶点v和v' 相关联。顶点v的度(degree) 是和顶点v相关联的边的数目,记为TD(v)。
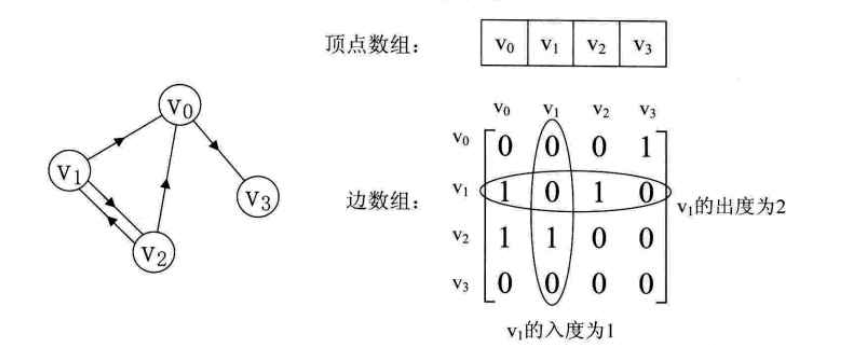
有向图G=(V, {E}), 对于弧<v,v'> , 顶点v邻接到v',顶点v'邻接自v。弧<v,v'> 和顶点v,v'相关联。以顶点v为头的弧数称为v的入度(InDegree),记为ID(v),以v为尾的弧的数目称为v的出度(OutDegree),记为OD(V)。顶点v的度TD(v)=ID(v)+ OD(v)。
简单路径,序列中顶点不重复。
简单环,除了第一个和最后一个,其余顶点不重复的回路,称为简单环。
连通图
无向图中,从v到v'有路径,则称v和v'是连通的。如果对于图中任意两个顶点都是连通的,则称为连通图。
无向图中的极大连通子图称为连通分量。
- 是子图
- 子图是连通的
- 连通子图还有极大顶点数
- 具有极大顶点数的连通子图包含依附于这些顶点的所有边
有向图中,如果对于每一对顶点都存在路径,则G是强连通图。
有向图中的极大强连通图称为强连通分量。
生成树
一个连通图的生成树是一个极小的连通子图,图中包括全部的n个顶点,但只有足已构成一条树的n-1条边。
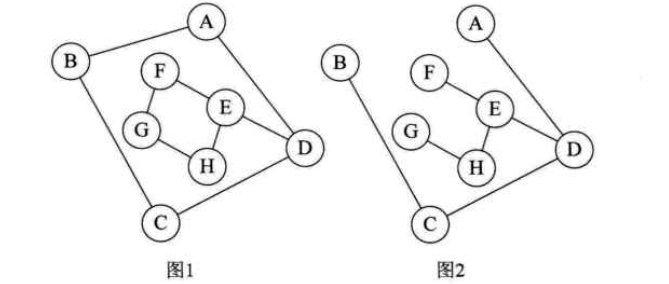
如果一个有向图恰好有一个顶点的入度为0,其余顶点的入度均为1,则是一棵有向树。
有向图的生成森林由若干有向树组成,含有全部顶点,但只有足以构成若干棵不相交的的有向树的弧。
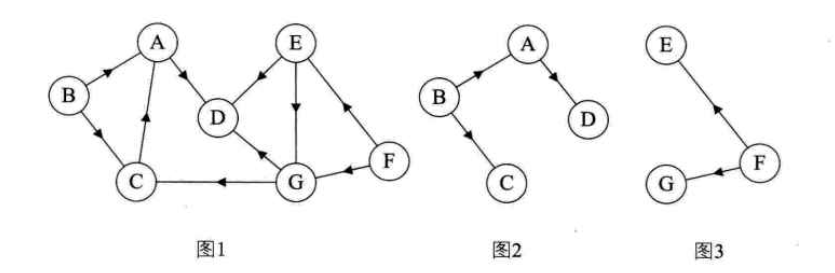
定义,术语总结

图的存储结构
邻接矩阵
图的邻接矩阵(Adjacency Matrix)由两个数组表示。
一个一维数组存储图中的顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧信息。
无向图
对称矩阵:
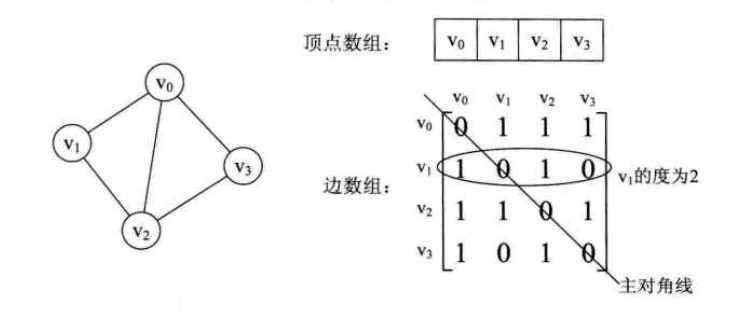
- 很容易判断两顶点是否有边
- 某个顶点的度,就是顶点所在行(或列)的元素之和
- 查询某个顶点的邻接点-把矩阵中第i行的元素扫描一遍,arc[i][j] 为1 就是邻接点
有向图
邻接表
邻接矩阵对于顶点较少的图,存储空间浪费问题。
数组与链表结合的存储方法 - 邻接表(adjancency list)
- 图中顶点用一维数组存储,每个顶点存储一个指针指向第一个邻接点
- 每个顶点的邻接点组成一个链表
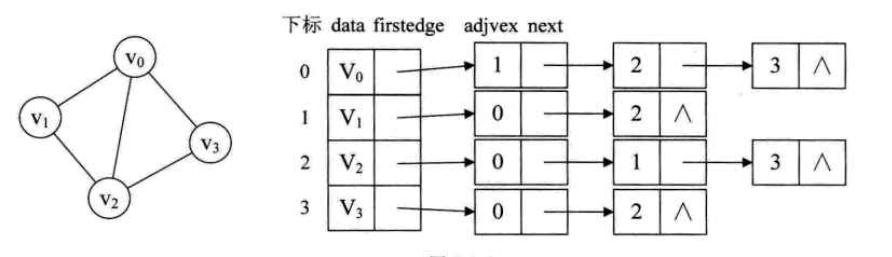
顶点结点由data和firstedge两个域组成,data存储数据,firstedge指向该顶点的第一个邻接点。
边表结点由adjvex 和 next组成,adjvex是邻接点的下标,next存储边表中下一个结点的指针。
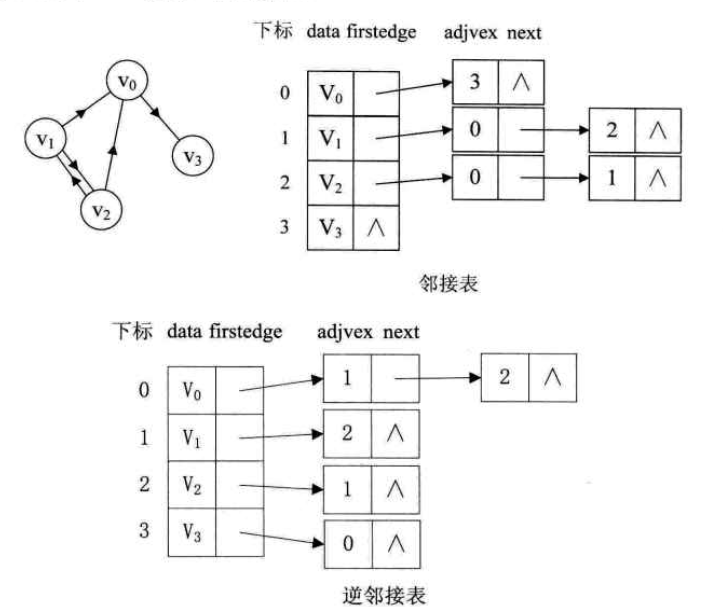
有向图的邻接表类似,以顶点的弧尾存储边表;逆邻接表,对每个顶点以弧头简历边表。
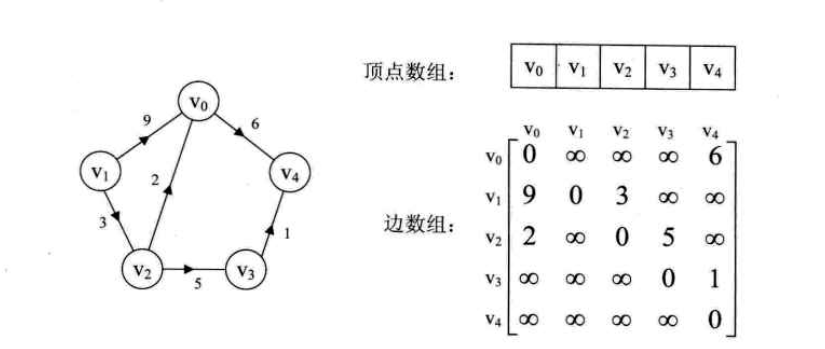
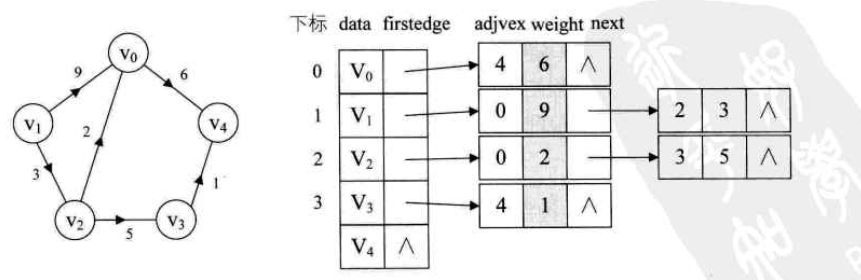
带权的网图,可以在边表结点中再增加weight域。
十字链表
邻接表的同一种结构只关心出或者入度。
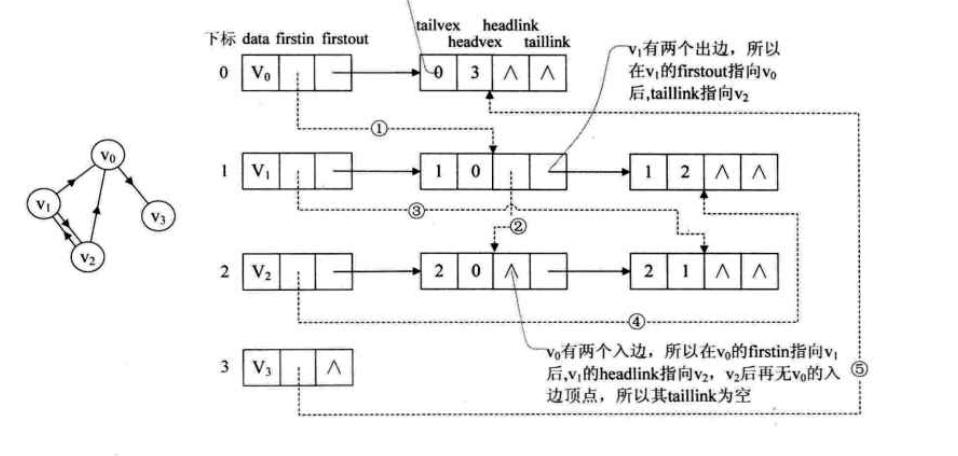
十字链表 - 结合邻接表与逆邻接表。
顶点表结点

firstin指向该顶点入边表中的第一个结点,firstout指向该顶点出边表中的第一个结点。
边表结点

- tailvex:弧起点在顶点表的下标
- headvex:弧终点在顶点表的下标
- headlink:指向终点相同的下一条边
- taillink:指向起点相同的下一条边
如果是网,添加一个weight域存储权值。
邻接多重表(无向图)
边表结点

ivex,jvex是与某条边依附的两个顶点下标;ilink指向依附于ivex的下一条边,jlink指向依附jvex的下一条边。 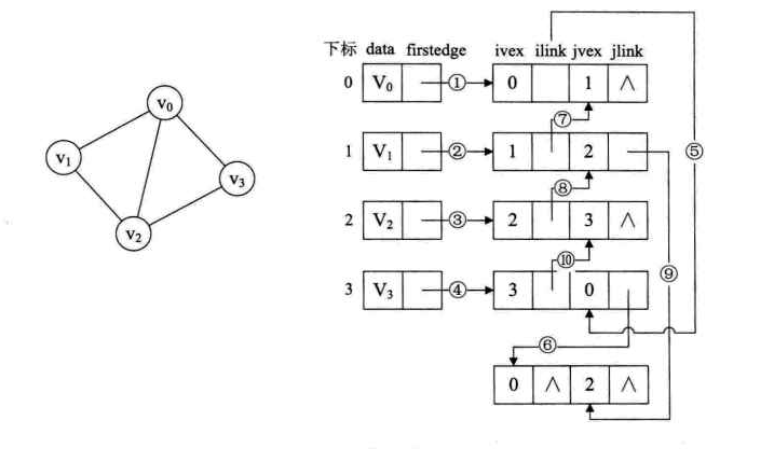
边集数组
两个一维数组:
- 存储顶点
- 存储边信息,有起点(begin),终点(end)和权(weight)
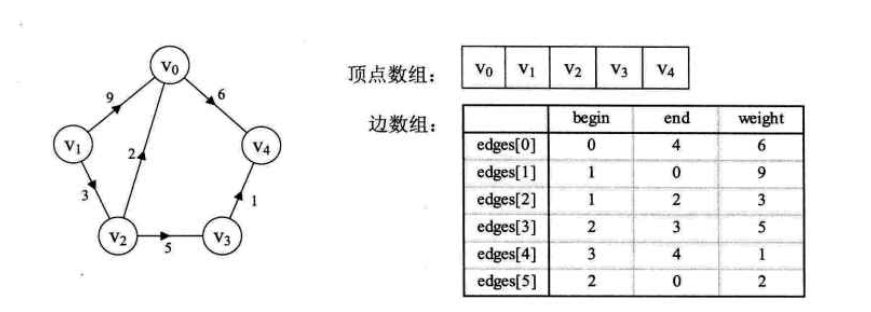
边集数组更关注边,边集数组中查找一个顶点发的度要扫描整个边数组,效率不高。因此适合对边的依次处理,不适合对顶点的操作。
图的表示
Post not found: 学习笔记之图的表示 学习笔记之图的表示图的遍历
从某一顶点出发访遍图中其余顶点,且每个顶点仅被访问一次,这个过程叫图的遍历(traversing graph)
深度优先遍历
DFS
广度优先遍历
BFS
图的典型算法
To Be Continue...