学习笔记之堆

学习笔记之堆

堆 heap

• 堆是一个完全二叉树
• 堆的每个节点值必须大于（或小于）其子树中每个节点的值

对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做“小顶堆”。

堆的实现

完全二叉树比较适合用数组来存储

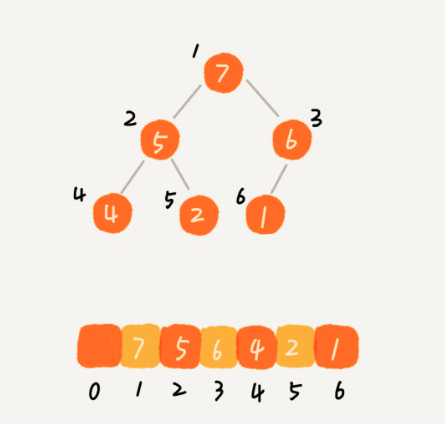
找到最后一个非叶子节点，在所有非叶子节点持续heapify。

eg - 构造大顶堆

public class HeapBuilder {

  static void heapify(int[] arr, int n, int i) {

    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;

    if(left < n && arr[left] > arr[largest]) {
      largest = left;
    }

    if (right < n && arr[right] > arr[largest]) {
      largest = right;
    }

    // if largest is NOT root
    if (largest != i) {

      int swap = arr[i];
      arr[i] = arr[largest];
      arr[largest] = swap;

      // recursive heapify the affected sub-tree
      heapify(arr, n, largest);
    }

  }

  static void buildHeap(int[] arr) {
    int length = arr.length;

    int startIdx = (length / 2) - 1;
    for (int i = startIdx; i >= 0; i--) {
      heapify(arr, length, i);
    }
  }

  static void printHeap(int[] arr) {

    for (int i = 0; i < arr.length; i++) {
      System.out.print(arr[i] + " ");
    }
    System.out.println();
  }

  public static void main(String[] args) {
    int arr[] = { 1, 3, 5, 4, 6, 13, 10,
                 9, 8, 15, 17 };
    buildHeap(arr);
    printHeap(arr);
  }


}

堆的应用

1. Java 中priorityQueue

合并小文件

例如合并多个有序的小文件

简单方法： 取每个小文件的第一个字符放到数组，比较大小，把最小取出来放入大文件，从数组中删除

改进： 每次找最小需要遍历数组，可使用优先队列（堆）代替。

高性能定时器

如果定期扫描（例如： 每秒扫描） 效率低

• 无用扫描 - 任务执行时间离当前时间比较远
• 扫描整个任务列表，耗时

优先队列： 小顶堆，顶部是最早执行的任务，这样定时器等待T（T为当前时间与队首任务的差值），取出元素并计算下一个等待时间。

2. Top K

维护K+1大小的小顶堆，遍历数组，不断插入元素到堆 , 如果堆大小超过K，则插入后删除一个元素

Post not found: 算法题-TopNFrequent 算法题-TopNFrequent

3. 中位数

静态数据： 中位数是固定的，先排序（只需一次）然后找到中位数

动态数据： 效率较低，每次查找都需要排序并重新计算下标。

借助堆：

一个大顶堆存放前n/2，一个小顶堆存放后n/2， 大顶堆的堆顶元素就是中位数。

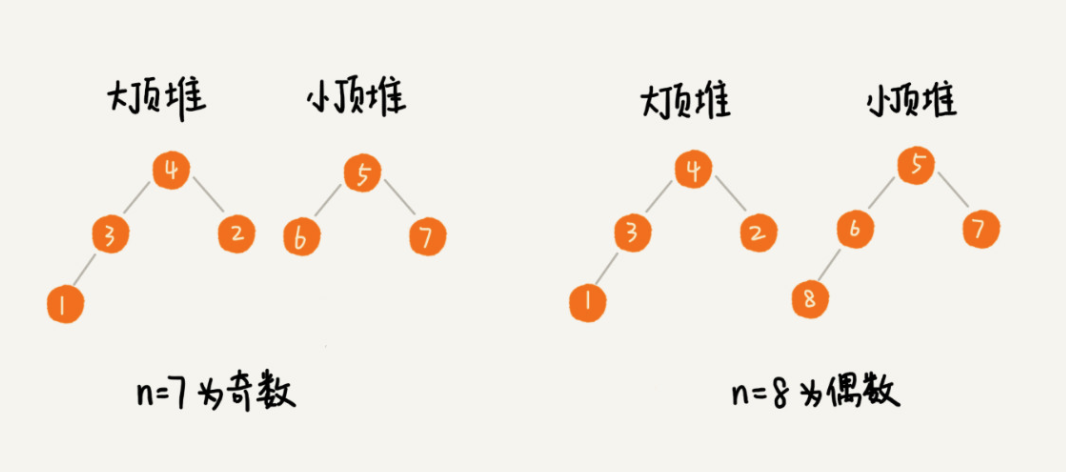
如果新加入的数据小于等于大顶堆的堆顶元素，我们就将这个新数据插入到大顶堆；否则，我们就将这个新数据插入到小顶堆。这个时候就有可能出现，两个堆中的数据个数不符合前面约定的情况：如果 n 是偶数，两个堆中的数据个数都是 2n；如果 n 是奇数，大顶堆有 2n+1 个数据，小顶堆有 2n 个数据。这个时候，我们可以从一个堆中不停地将堆顶元素移动到另一个堆，通过这样的调整，来让两个堆中的数据满足上面的约定。

查看 Post not found: 算法题-中位数 算法题-中位数

---

参考：

https://www.geeksforgeeks.org/building-heap-from-array/